Understanding the Dilutive Impact of Warrants
One of the most confusing aspects of warrant pricing is dilution, but there’s no way around it. If your company is thinking about issuing warrants, or already has some outstanding, the impact of dilution is something you’ll need to know about. Beyond that is the question of whether dilution even matters—and, if it does, which valuation model to use.
We’ll get into all of that in a moment. Before we do, though, let’s look at what makes warrants different from plain vanilla and employee stock options.
The Difference Between Warrants and Options
Warrants are securities that have payoffs similar to plain vanilla traded call options, but a dilution impact when exercised, similar to employee stock options. To understand this better, consider what happens when each type of security is exercised.
When someone exercises a regular exchange-traded call option, it has no effect on the number of common shares outstanding. If the option writers don’t own the company’s shares, they have to buy them from the market so they can deliver. But the company doesn’t issue more shares.
When someone exercises a warrant, however, the company issues more shares and then sells them to the warrant holder for the strike price. As the strike price is less than the market price of the stock, this dilutes the interest of the existing shareholders.
Employee stock options are call options on company stock that the company grants to its employees. But when employees exercise them, they buy the option shares from the company at a discount to the market price. So in terms of the dilution impact, they’re similar to warrants.
Warrants and employee stock options have another thing in common. In each case, the company predetermines the number of options it issues. That’s different from exchange-traded options, where the number isn’t subject to the company’s decisions. Instead, individual investors write new options, causing the number of options outstanding (also known as the open interest) to go up. As people close out positions, open interest goes down.
The Role of Dilution
With that, let’s turn our attention to the valuation of outstanding warrants. How should potential dilution factor in? The answer depends on whether the company is public or private. It also depends on the types of warrants to be issued.
Public company scenario. Suppose a public company announces its intention to issue warrants for the next round of financing. An efficient market will react to the announcement so that the stock price immediately reflects the potential dilution from the yet-to-be-issued warrants. This dilution impact might not be visible since warrants are typically bundled with other transactions (or otherwise sold to investors). Regardless, the warrant’s value should equal the value of a call option with the same strike and maturity.
However, if investors don’t know about the warrant issuance, then the stock price at issuance and the volatility both have to be adjusted to reflect the surprise of the unknown warrants.
Private company scenario. Now suppose it’s a private company that wants to issue warrants. In this case, the yet-to-be-issued warrants will reduce the current stock price given the cost of issuing warrants. In other words, the warrants will be worth less than regular call options with the same strike and maturity.
In this scenario, a diluted Black-Scholes-Merton (BSM) model is more appropriate for determining the valuation. Alternatively, the Option Pricing Model (OPM) could work, as this framework incorporates the dilution impact from the warrants.
Models for Incorporating Dilution
Now we get into the mechanics of incorporating dilution. There are multiple models available. The one you use should be a careful choice based on the circumstances, noting that different models may have different results. Keep in mind that with warrants, it’s important to think about whether the market has reacted to its issuance. Also, the choice of model can have a large impact for larger warrant issuances. In other words, extra judgement may be required in how you build dilution into your warrants.
To see a few examples, click “details” below.
Model 1
At time 0. Consider the situation where a company is weighing a new issue of warrants. We suppose that the company is interested in calculating the cost of the issue, assuming that there are no compensating benefits. So the assumptions are:
- The company has N shares worth S0
- Warrants to be granted is M
- Strike price is K
The value of the company today is N*S0. This value stays the same even with the warrant issue.
At time T. Suppose that, without the warrant issuance, the share price is St at the warrant’s maturity. This means that (with or without the warrant issuance) the total value of the equity and the warrants at time T will be N*St.
If the warrants are exercised, there is a cash inflow from the strike price increasing this to N*St + M*K. This value is distributed among (M+N) shares, so that the share price immediately after exercise becomes
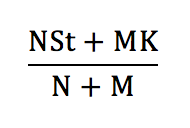
Therefore, the payoff to an option holder if the option is exercised is
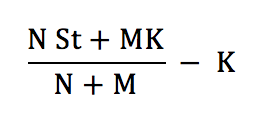
or
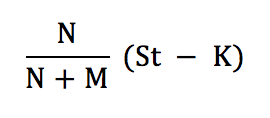
This shows that the value of each option is the value of

Therefore the total cost of the warrants is M times this.
Since we’re assuming that there are no benefits to the company from the warrant issue, the total value of the company’s equity will decline by the total cost of the options as soon as the decision to issue the warrants becomes generally known.
The total cost of the warrant issue, then, is
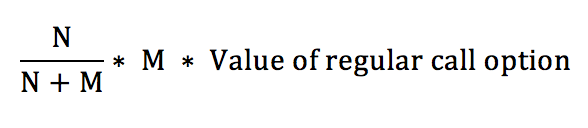
which means that the reduction in the stock price is
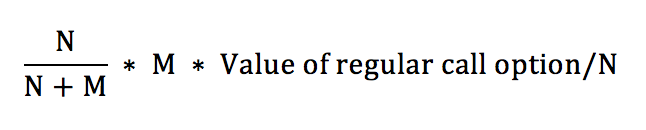
For more information, see John C. Hull’s Options, Futures, and Other Derivatives (9th edition).
Model 2
The Black-Scholes formula, with some adjustments for the impact of dilution, can be used to value European warrants issued by a company on its own stock. This includes a dilution factor plus an adjusted stock price and volatility. So:
- The stock price S0 is replaced by S0 + (M/N)*W, with W being the warrant price
- The volatility is the volatility of the equity of the company (i.e., it’s the volatility of the value of the shares plus the warrants—not just the shares)
- The formula is multiplied by N/(N+M)
For more, see John C. Hull’s Options, Futures, and Other Derivatives (5th edition).
Model 3
The Option Pricing Model is typically used for private companies. That said, it can also be used for public companies by backsolving for the stock price. Using a series of call options, the OPM allocates the enterprise value of the company to each security based on the proportional value at each point in the capital structure. This methodology is especially useful if there are multiple classes of warrants, as it ascribes specific dilution from each.
For more, see AICPA’s Practice Aid on Valuation of Privately-Held Company Equity Securities Issued as Compensation.
No doubt about it: Dilution in warrant pricing can be confusing. We hope this post sheds some light on the subject, though. If you have questions or would like to talk this through, please contact us—we’re happy to help.

